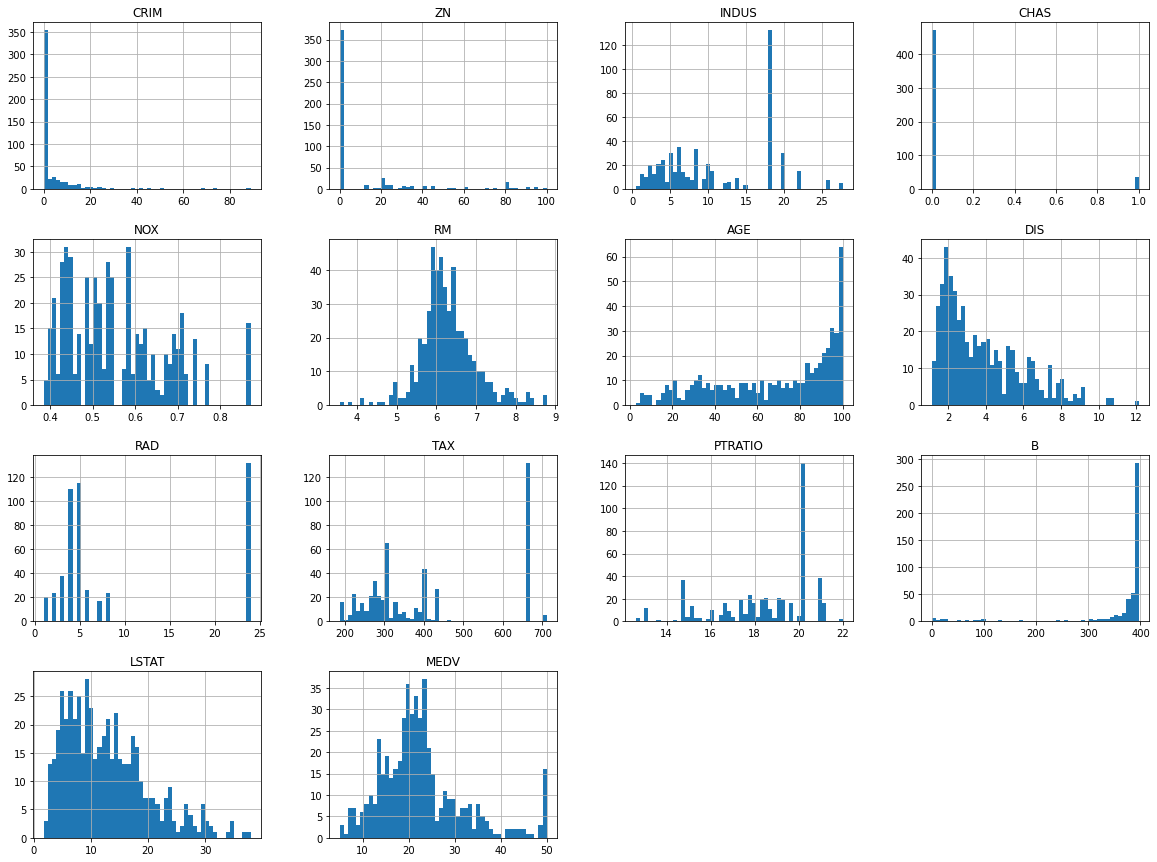
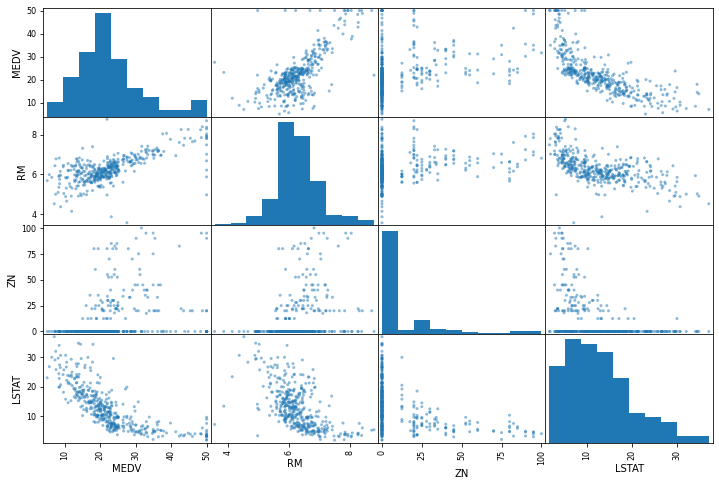
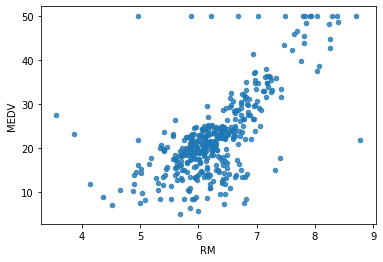
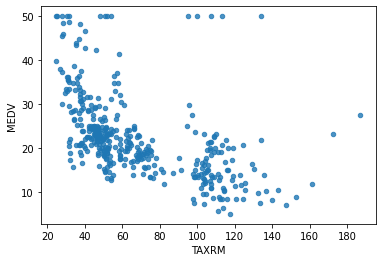
array([[-0.43942006, 3.12628155, -1.12165014, ..., -0.97491834,
0.41164221, -0.86091034],
[-0.44352175, 3.12628155, -1.35893781, ..., -0.69277865,
0.39131918, -0.94116739],
[ 0.15682292, -0.4898311 , 0.98336806, ..., 0.81196637,
0.44624347, 0.81480158],
...,
[-0.43525657, -0.4898311 , -1.23083158, ..., -0.22254583,
0.41831233, -1.27603303],
[ 0.14210728, -0.4898311 , 0.98336806, ..., 0.81196637,
-3.15239177, 0.73869575],
[-0.43974024, -0.4898311 , 0.37049623, ..., -0.97491834,
0.41070422, 0.09940681]])